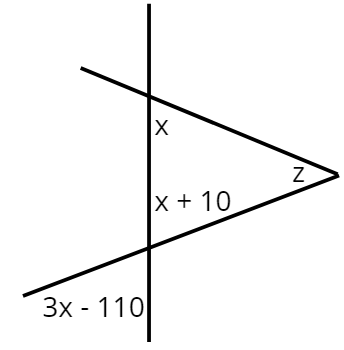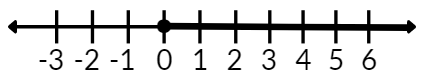Ejercicios 16 al 30 de opción múltiple
A continuación, encontrarás 15 ejercicios de opción múltiple con un formato y nivel de dificultad similar al de la prueba oficial. Para simular las condiciones de la prueba, puedes configurar un temporizador digital de 16 minutos y 25 segundos en tu teléfono móvil, que es el tiempo que tendrías para contestar 15 preguntas de esta sección. Esto significa que debes tratar de responder cada pregunta en un máximo de 65 segundos. Si no logras responder una pregunta en este lapso, avanza a la siguiente para asegurarte de responder todas las preguntas que puedas. Si todavía te queda tiempo disponible al final, puedes regresar y revisar las preguntas que dejaste en el camino.
Para comenzar el cuestionario, desliza hacia abajo, encontrarás las preguntas por debajo de estas instrucciones. Para finalizar el cuestionario y ver tus resultados da clic en el botón «Terminar Cuestionario» que se encuentra al final de la página.
Puedes tomar el cuestionario las veces que quieras dando clic en el botón «Reiniciar». Si deseas ver la explicación a cada respuesta, haz clic en el botón «Ver respuestas» que aparece después de terminar el cuestionario.
Resumen de Examen
0 de 15 Preguntas completado
Preguntas:
Información
Ya has completado el examen antes. Por lo tanto, no puede iniciarlo de nuevo.
Examen está cargando…
Debe iniciar sesión o registrarse para iniciar el examen.
Primero debe completar lo siguiente:
Resultados
Resultados
0 de 15 Preguntas respondió correctamente
Tu tiempo:
ha pasado el tiempo
Categorías
- No categorizado 0%
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- Actual
- Revisar
- Contestada
- Correcto
- Incorrecto
-
Pregunta 1 of 15
1. Pregunta
16. Una piscina tiene una forma rectangular y mide 20 metros de largo por 10 metros de ancho. La función que describe el volumen de agua en la piscina en función de la profundidad del agua es: f(x) = 20 * 10 * x. ¿Cuántos metros cúbicos de agua hay en la piscina si la profundidad es de 2 metros?
CorrectoIncorrecto -
Pregunta 2 of 15
2. Pregunta
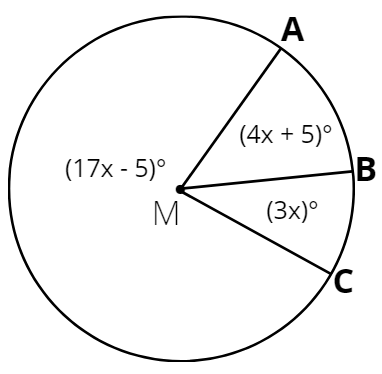
17. En la figura anterior, M es el centro del círculo. ¿Cuál es la medida del arco AC?
CorrectoIncorrecto -
Pregunta 3 of 15
3. Pregunta
18. Si dos ángulos son complementarios y uno mide 2x grados, ¿Cuál es la medida del otro ángulo en términos de x?
CorrectoIncorrecto -
Pregunta 4 of 15
4. Pregunta
19. En la figura anterior, ¿Cuántos grados vale z?
CorrectoIncorrecto -
Pregunta 5 of 15
5. Pregunta
20. Un cubo tiene una arista de 5 metros. ¿Cuál es su volumen en metros cúbicos?
CorrectoIncorrecto -
Pregunta 6 of 15
6. Pregunta
21. En un parque de atracciones, el 40% de los visitantes hace el paseo en barco, el 25% hace el paseo en montaña rusa y el 15% hace ambos paseos. Si se selecciona al azar a uno de los visitantes, ¿Cuál es la probabilidad de que NO haga ni el paseo en barco ni el de montaña rusa?
CorrectoIncorrecto -
Pregunta 7 of 15
7. Pregunta
22. Una caja tiene 5 cartas de diferentes figuras. ¿De cuántas formas diferentes se podrían colocar sobre la mesa si importa el orden?
CorrectoIncorrecto -
Pregunta 8 of 15
8. Pregunta
23. Un ingeniero está diseñando un sistema de riego para un parque. El sistema debe contar con un motor de potencia 100. ¿Cómo puede el ingeniero descomponer en factores primos el número 100 para poder determinar qué tipo de motor debe utilizar?
CorrectoIncorrecto -
Pregunta 9 of 15
9. Pregunta
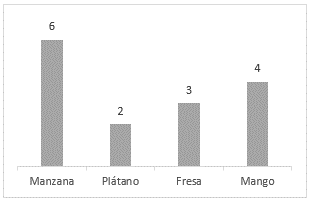
24. La gráfica anterior representa la cantidad de frutas que un chef tiene disponibles para preparar una ensalada para un banquete. El chef elige una fruta al azar para cortar y agregar a la ensalada, ¿Cuál es la probabilidad de elegir una fresa en una selección?
CorrectoIncorrecto -
Pregunta 10 of 15
10. Pregunta
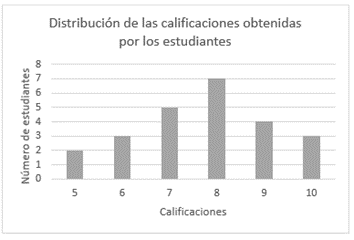
25. La gráfica anterior representa la distribución de las calificaciones obtenidas por un grupo de estudiantes en un examen de matemáticas, ¿Cuál es la moda de las calificaciones obtenidas por los estudiantes?
CorrectoIncorrecto -
Pregunta 11 of 15
11. Pregunta
26. La figura anterior muestra la solución gráfica de:
CorrectoIncorrecto -
Pregunta 12 of 15
12. Pregunta
27. Laura pone dinero en su cuenta de ahorro de la siguiente manera: la primera semana deposita $20, y en cada una de las siguientes semanas deposita $10 más solamente. ¿Cuántas semanas se requieren para que Laura tenga $200 en su cuenta de ahorro?
CorrectoIncorrecto -
Pregunta 13 of 15
13. Pregunta
28. Si 6x + 3y = 15, entonces y=
CorrectoIncorrecto -
Pregunta 14 of 15
14. Pregunta
29. Si un auto recorre 120 km en 2 horas a una velocidad de 60 km/h, ¿Cuántas horas se necesitarán para recorrer la misma distancia si su velocidad es de 30 km/h?
CorrectoIncorrecto -
Pregunta 15 of 15
15. Pregunta
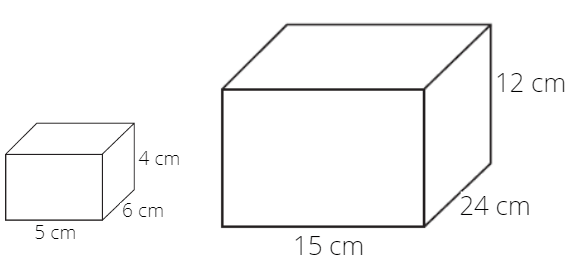
30. La figura anterior muestra las dimensiones de una caja y un contenedor respectivamente, ¿Cuántas cajas caben en el contenedor?
CorrectoIncorrecto